Square Thread Definition, Uses, Angle, Calculation, Standard and Dimensions Chart

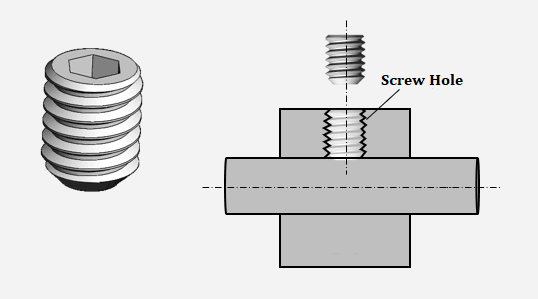
Threads are crucial components in the engineering field, different types of screw threads are applied for fastening, power transmission, and other purposes. One of the important screw threads we are going to explore is the square thread. This article covers its definition, profile features, uses, angle, diagram, dimensions chart, and more.

What Is Square Thread?

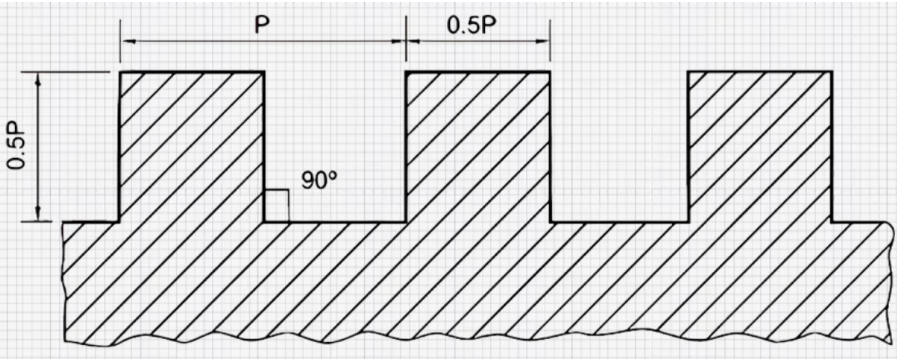
The square thread is a common type of screw thread form or profile. Its cross-sectional shape is square, with the sides, root, and crest of any section formed by a plane passing through the thread axis theoretically equal to one half of the pitch. The thread flanks are perpendicular to the thread axis, the depth and thickness of the thread are equal to half the pitch, and the root and crest are 90°sharp corners.

Main features of a square thread profile include 0° angle, a flat crest of the external thread and the root of the internal thread, and the pitch diameter of square threads is the same as the nominal diameter minus half the pitch.

Advantages of square threads

• Higher efficiency than ACME or metric trapezoidal threads
• Extended life of nuts
• Low friction
• Increased clamping speed

Disadvantages of square threads

• Difficult to machine or manufacture
• Slow cutting as single-point cutting tools can’t get efficient rake and relief angles
• Can’t carry as much load as a trapezoidal thread
• Can’t compensate for wear on the nut
• Reduced minor pitch diameter
• Reduced thread root cross-section
• Increased cost

ACME Thread vs Square Thread

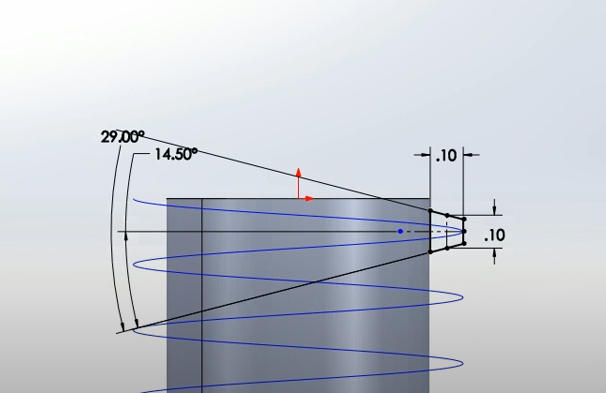
There are multiple threads that are used as screw threads for load carrying or precision motion applications. Square and ACME threads are two common types. ACME threads have a 29-degree angle, which makes them easier to machine and stronger than square threads (90-degree angle). ACME threads have a few advantages over other thread forms, which include square and V-threads. With their broader base, ACME screw threads have higher strength and wear resistance in comparison to V-threads.

Feature	ACME Threads	Square Threads
Thread Angle	29 degrees	90 degrees
Manufacturing	Easier to manufacture due to the angled root	More complex to manufacture
Strength	Generally stronger with the same dimensions	More efficient but less strong
Efficiency	Lower efficiency due to greater friction	Higher efficiency with lower friction

 

Square Thread Applications – What Are Square Threads Used For?

Screws with square threads are primarily used in applications that require high power transmission efficiency and high load capacity; typical examples are leadscrews and jackscrews. Square threads are also employed for purposes including attachment, clamping, adjustment, pressure application in machinery, and coupling components, while withstanding tensile or shear stresses based on the specific uses.

Square screw threads are usually found in precision measuring instruments, aerospace equipment, and robotics.

Square Thread Standards

Square thread dimensions are specified in ISO standards. Sq represents a square thread, with the nominal diameter and the pitch in millimeters (mm). For example, Sq60 x 9 indicates a square thread with a nominal diameter of 60 mm and a pitch of 9 mm. When there is no suffix, it denotes a single-start thread. If a suffix is included, the value after the multiplication sign refers to the lead, and the value in parentheses indicates the pitch. For instance, Sq40×8(P4) would denote a double-start thread (lead divided by the pitch is 2).

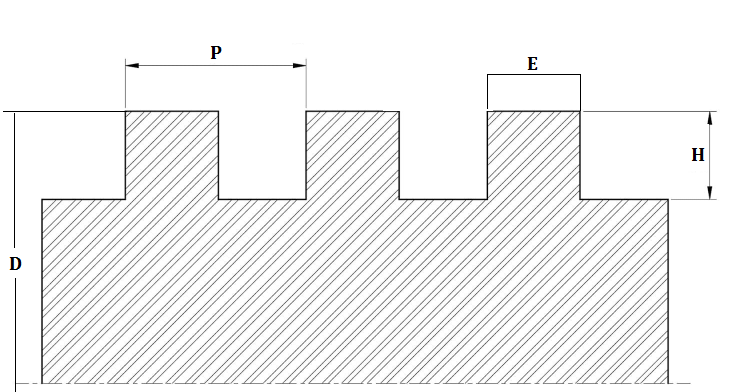
Square Thread Angle & Diagram

Unlike other screw thread types, square threads are characterized by having a thread angle of 0 degrees. The angle of V-threads is 60°, and ACME threads have a 29° angle.

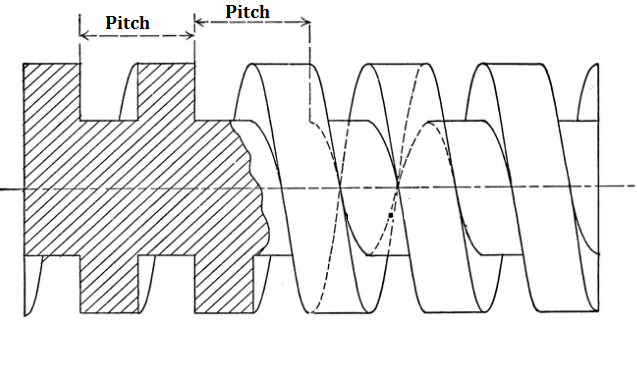
Square Thread Calculation Formula

1. P=0.2D

P is the pitch of square screw thread, D is the outside diameter of the screw (major diameter)

2. E=0.5P

E is the thickness of the thread

3. H=0.5P

H is the height of the thread

4. d=D-2H

d is the inside diameter of the screw (minor diameter)

5. D1=d+0.125P

D1 is the diameter for turning the nut

How to Measure and Calculate Square Thread Pitch?
To figure out the pitch of a square thread, you must measure the distance between two adjacent crests or valleys of the thread. A caliper or a ruler is needed. This result can be calculated by dividing the thread length by the total number of threads.

To measure the square thread pitch, first choose two neighboring crests or two adjacent valleys, then use a caliper or ruler to measure the distance between the two points. The pitch is the distance between corresponding points on adjacent threads.

You can also measure the thread length and calculate the pitch with the formula: P = L / n, where P is the thread pitch, L represents thread length, and n stands for the number of threads. The distance you calculated is the pitch of the square thread. It is available in millimeters with the metric system and in inches with the imperial system.

Square Thread Dimensions Chart

Here is a square thread chart that lists dimensions in inches. Select the appropriate pitch based on factors such as transmission speed and load capacity. The depth of the thread and the width of the thread bottom space are both equal to half of the pitch.

Threads per Inch	Pitch (Inches)	Depth of Thread	Double Depth of Thread	Width of Top of Thread	Width of Space at Bottom of Thread
1	1.0000	.5000	1.0000	.5000	.5000
1 1/3	.7500	.3750	.7500	.3750	.3750
1 1/2	.6667	.3333	.6667	.3333	.3333
1 3/4	.5714	.2857	.5714	.2857	.2857
2	.5000	.2500	.5000	.2500	.2500
2 1/2	.4000	.2000	.4000	.2000	.2000
3	.3333	.1676	.3333	.1667	.1667
3 1/2	.2857	.1429	.2857	.1429	.1429
4	.2500	.1250	.2500	.1250	.1250
4 1/2	.2222	.1111	.2222	.1111	.1111
5	.2000	.1000	.2000	.1000	.1000
5 1/2	.1818	.0909	.1818	.0909	.0909
6	.1667	.0833	.1667	.0833	.0833
7	.1429	.0714	.1429	.0714	.0714
8	.1250	.0625	.1250	.0625	.0625
9	.1111	.0556	.1111	.0556	.0556
10	.1000	.0500	.1000	.0500	.0500
11	.0909	.0455	.0909	.0455	.0455
12	.0833	.0417	.0833	.0417	.0417
13	.0769	.0385	.0769	.0385	.0385
14	.0714	.0357	.0714	.0357	.0357
15	.0667	.0333	.0667	.0333	.0333
16	.0625	.0312	.0625	.0312	.0312
18	.0556	.0278	.0556	.0278	.0278
20	.0500	.0250	.0500	.0250	.0250
22	.0455	.0227	.0455	.0227	.0227
24	.0417	.0208	.0417	.0208	.0208